20世纪70年代，美国匹兹堡大学教授T.?L.?Saaty在负责美国国防部的一个关于电力分配课题时，发现课题中各种影响因素相互作用，而且子因素众多，由于当时时间上、数据量上都明显不足，Saaty教授构建了一种定性分析与定量分析相结合、无需大量数据统计的结构化模型——层次分析法（Analytic Hierarchy Process，简称AHP）。通过将层次中各因素成对比较而确定相对重要度，然后在结合了人为判断的情况下，确定各因素相对重要性的排序，不仅很好地完成了当时的课题，而且于1977年在第一届国际数学建模会议上正式提出，引起学术界的关注。层次分析法属于运筹学范畴，是一种多目标决策方法，广泛应用于科学研究和生产实践中。

层次分析法（AHP）是为了达成决策目的，将与目标相关的因素划分为目标、准则、方案三个层次，通过构造成对比较矩阵，在层次中定性分析出各因素的相对重要度，最终通过计算确定各个因素的权重。AHP的实施步骤：

1.?对问题所涉及的因素进行分类，构造一个各因素之间相互关联的层次结构模型。处于最上层的是预定目标，中间层元素是准则（或有子准则），最底层一般是解决方案。如图1-1所示。

?

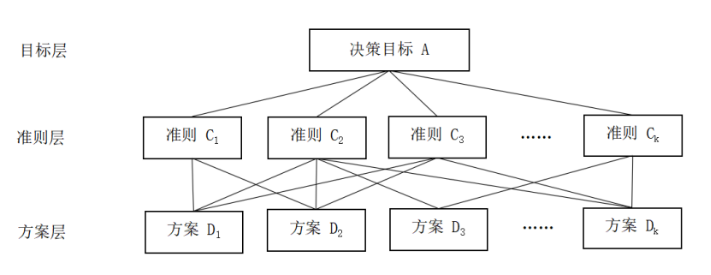
2.?构造成对比较矩阵。成对比较的元素aij表示的是第i个因素相对于第j个因素的比较结果，这个值使用的是Santy的1-9标度方法。如图1-2。由判断矩阵计算被比较元素相对权重。

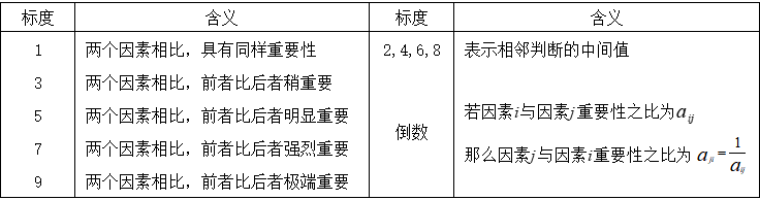
3.?层次排序与一致性检验。计算判断矩阵的最大特征值λ_max，并判断矩阵的偏差一致性指标CI。

其中n为判断矩阵阶数。随机一致性比：

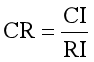
RI是平均随机一致性指标，根据表1-1可查各矩阵阶数对应的值。计算结果CR＜0.1时，判断矩阵的一致性合格，反之则需要对判断矩阵进行调整。

?

表1-1矩阵阶数与RI值对照表

?

本文为冠卓咨询原创文字作品，任何人或组织不得对本文进行篡改，转载或以盈利为目的行为，一经发现，将负法律责任。